The previous post introduced the nuances related to communication between GPUs. This post will look into common communication operations used when training on multiple GPUs.
Let’s take a closer look at different communication operations. Before looking at the operations, we will look at how to run distributed code using PyTorch.
import torch.distributed as dist
def init_distributed(backend="nccl"):
"""Initialize the distributed environment."""
dist.init_process_group(backend=backend)
def run():
"""Distributed function."""
rank = dist.get_rank()
world_size = dist.get_world_size()
print(f"Hello from rank {rank} out of {world_size} processes!")
def main():
init_distributed()
run()
dist.destroy_process_group()
if __name__ == "__main__":
main()
Run this script using torchrun command,
torchrun --nnodes=1 --nproc_per_node=4 hello_dist.py
# Expected output on a 1 node with 4 GPUs (Note that the rank messages can be printed out of order):
Hello from rank 1 out of 4 processes!
Hello from rank 3 out of 4 processes!
Hello from rank 0 out of 4 processes!
Hello from rank 2 out of 4 processes!
There are multiple approaches to invoke the distributed script and the code might have to change slightly depending on the implementation. There is torch.multiprocessing.spawn which is a low-level API. It expects the user to pass the correct environment variables like master address, master port, rank and world_size. On the other hand, torchrun which is a higher abstraction takes care of setting all these up for you automatically. The only input it requires is to select the backend required for running the distributed code.
Going back to the code, there are two functions
init_distributed: This function creates process groups on each worker (GPU or CPU). It also uses rank 0 as master and initializes all ranks so they are ready to communicate with each other through master.run: A simple example where we print the local rank and print a hello message from that particular rank.
There is a terminology used when it comes to distributed computing. Following are few popular ones
- Node: a single machine in the cluster
- Rank: unique identifier for each process in the group
- Local Rank: rank ID of a process within its node
- Global Rank: rank ID across all nodes
- World size: total number of processes
Point to point
Point to point communication involves directly send the data to the desired GPU. This operation uses send and recv functions under torch.distributed API. These operations are synchronous or blocking until the operation completes. There are asynchronous equivalents of these functions isend and irecv that provide non-blocking communication.
Pipeline parallelism uses point to point communication to send the activations to next GPU that has subsequent layers.
import os
import torch
import torch.distributed as dist
def init_process():
dist.init_process_group(backend="nccl")
local_rank = int(os.environ["LOCAL_RANK"])
torch.cuda.set_device(local_rank)
def example_send_recv():
rank = dist.get_rank()
local_rank = int(os.environ["LOCAL_RANK"])
if rank == 0:
# Rank 0 creates a tensor and sends it to rank 1
tensor = torch.tensor([42.0], device=local_rank)
print(f"Rank {rank} sending: {tensor.item()}")
dist.send(tensor, dst=1)
elif rank == 1:
# Rank 1 prepares an empty tensor and receives from rank 0
tensor = torch.zeros(1, device=local_rank)
print(f"Rank {rank} before receiving: {tensor.item()}")
dist.recv(tensor, src=0)
print(f"Rank {rank} received: {tensor.item()}")
else:
# Other ranks do nothing
print(f"Rank {rank} idle.")
if __name__ == "__main__":
init_process()
example_send_recv()
dist.destroy_process_group()
Running the example produces following output
torchrun --nproc_per_node=4 send_recv_demo.py
# Expected output (order may vary slightly):
Rank 2 idle.
Rank 3 idle.
Rank 0 sending: 42.0
Rank 1 before receiving: 0.0
Collective communication
While point-to-point communication is flexible and used in pipeline parallelism, most training workloads rely on collective operations that involve all GPUs.
PyTorch provides out of box implementations for communication collectives that are used widely in distributed setting. Following are the links to collection of supported backends, collectives and operators
- Collectives such as broadcast, reduce, all_reduce
- Operators such as sum, max, prod, min
- Backends such as
glooandncclalong with the supported collectives for each backend
I highly recommend interested readers to read a detailed paper on NCCL that shades a mega flash light on the internals on NCCL workings and implementation of the collective operations.
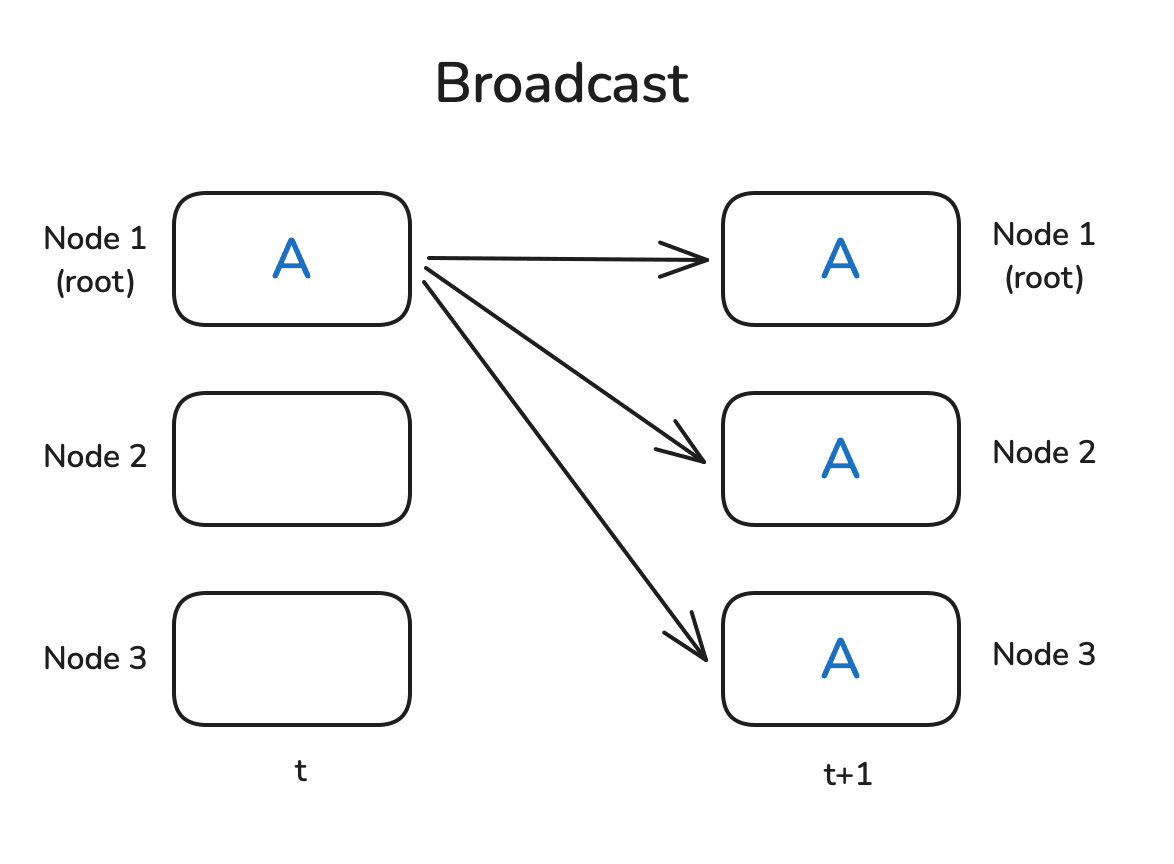
Broadcast
Broadcast as name implies transfers data from rank 0 to all ranks. Since all the data has to get out of rank 0 the communication is bottlenecked by the bandwidth of the master rank.
To overcome this limitation, NCCL uses ring topology where master (root) sends data to its next successor and so on. This process continues until the data reaches the last GPU in the chain.
import os
import torch
import torch.distributed as dist
def init_process():
dist.init_process_group(backend="nccl")
local_rank = int(os.environ["LOCAL_RANK"])
torch.cuda.set_device(local_rank)
def example_broadcast():
rank = dist.get_rank()
local_rank = int(os.environ["LOCAL_RANK"])
if rank == 0:
tensor = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float32).cuda(local_rank)
else:
tensor = torch.zeros(5, dtype=torch.float32).cuda(local_rank)
print(f"Before broadcast on rank {rank}: {tensor}")
dist.broadcast(tensor, src=0)
print(f"After broadcast on rank {rank}: {tensor}")
if __name__ == "__main__":
init_process()
example_broadcast()
dist.destroy_process_group()
Here’s the expected output for broadcast operation:
Before broadcast on rank 3: tensor([0., 0., 0., 0., 0.], device='cuda:3')
Before broadcast on rank 1: tensor([0., 0., 0., 0., 0.], device='cuda:1')
Before broadcast on rank 2: tensor([0., 0., 0., 0., 0.], device='cuda:2')
Before broadcast on rank 0: tensor([1., 2., 3., 4., 5.], device='cuda:0')
After broadcast on rank 0: tensor([1., 2., 3., 4., 5.], device='cuda:0')
After broadcast on rank 2: tensor([1., 2., 3., 4., 5.], device='cuda:2')
After broadcast on rank 1: tensor([1., 2., 3., 4., 5.], device='cuda:1')
After broadcast on rank 3: tensor([1., 2., 3., 4., 5.], device='cuda:3')
Gather and All-gather
Gather as the name suggests simply gets all the data from all ranks to rank 0. Again similar to broadcast, rank 0 becomes the bottleneck since it must receive data from all the ranks.
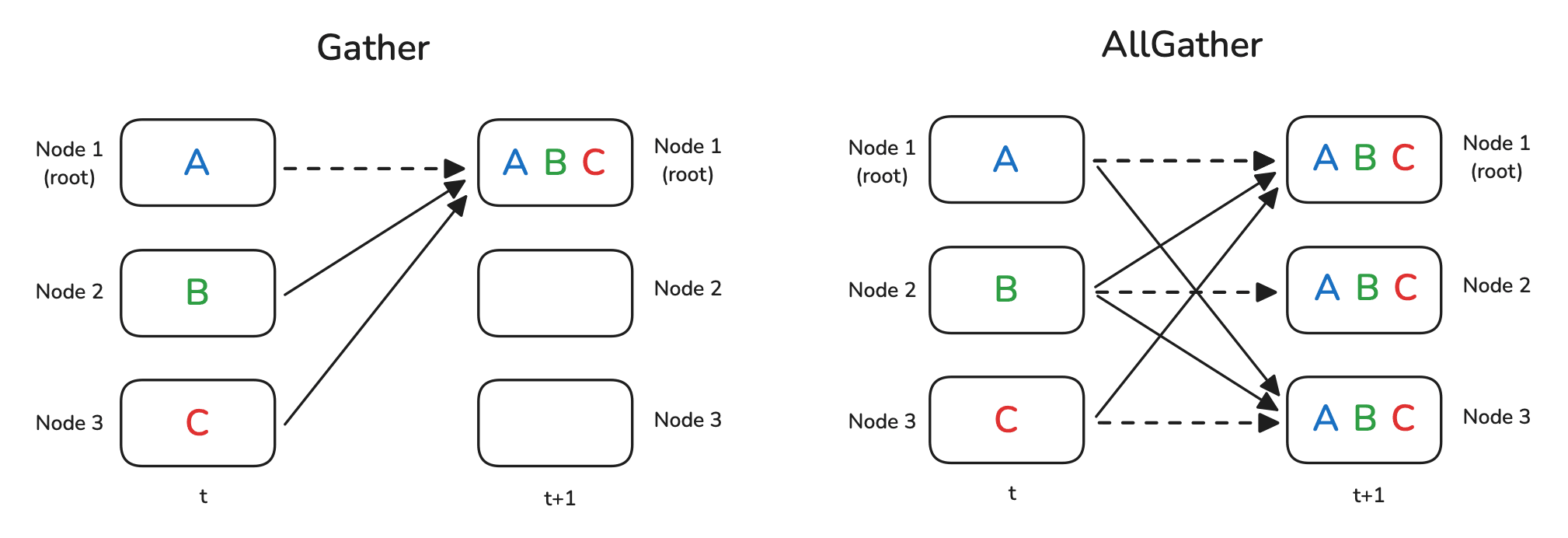
All-gather is used widely in data parallelism and ZeRO techniques. It expects all ranks to gather data from all ranks. The final result will be all ranks having same data. NCCL uses a ring topology for efficient communication and utilization of the network bandwidth. Each GPU sends data to its right-hand neighbor and it receives data from its left-hand neighbor.
import os
import torch
import torch.distributed as dist
def init_process():
dist.init_process_group(backend="nccl")
local_rank = int(os.environ["LOCAL_RANK"])
torch.cuda.set_device(local_rank)
def example_gather():
rank = dist.get_rank()
world_size = dist.get_world_size()
local_rank = int(os.environ["LOCAL_RANK"])
tensor = torch.tensor([rank], device=local_rank, dtype=torch.float32)
print(f"[Gather] Rank {rank} starts with: {tensor}")
# Only rank 0 will collect results
gather_list = [torch.zeros(1, device=local_rank) for _ in range(world_size)] if rank == 0 else None
dist.gather(tensor, gather_list=gather_list, dst=0)
if rank == 0:
print(f"[Gather] Rank 0 collected: {gather_list}")
def example_all_gather():
rank = dist.get_rank()
world_size = dist.get_world_size()
local_rank = int(os.environ["LOCAL_RANK"])
tensor = torch.tensor([rank], device=local_rank, dtype=torch.float32)
print(f"[All-gather] Rank {rank} starts with: {tensor}")
all_gather_list = [torch.zeros(1, device=local_rank) for _ in range(world_size)]
dist.all_gather(all_gather_list, tensor)
print(f"[All-gather] Rank {rank} collected: {all_gather_list}")
if __name__ == "__main__":
init_process()
example_gather()
example_all_gather()
dist.destroy_process_group()
Here’s the expected output for the gather and all-gather operations:
[Gather] Rank 0 starts with: tensor([0.], device='cuda:0')
[Gather] Rank 1 starts with: tensor([1.], device='cuda:1')
[Gather] Rank 2 starts with: tensor([2.], device='cuda:2')
[Gather] Rank 3 starts with: tensor([3.], device='cuda:3')
[All-gather] Rank 1 starts with: tensor([1.], device='cuda:1')
[All-gather] Rank 2 starts with: tensor([2.], device='cuda:2')
[All-gather] Rank 3 starts with: tensor([3.], device='cuda:3')
[Gather] Rank 0 collected: [tensor([0.], device='cuda:0'), tensor([1.], device='cuda:0'), tensor([2.], device='cuda:0'), tensor([3.], device='cuda:0')]
[All-gather] Rank 0 starts with: tensor([0.], device='cuda:0')
[All-gather] Rank 3 collected: [tensor([0.], device='cuda:3'), tensor([1.], device='cuda:3'), tensor([2.], device='cuda:3'), tensor([3.], device='cuda:3')]
[All-gather] Rank 1 collected: [tensor([0.], device='cuda:1'), tensor([1.], device='cuda:1'), tensor([2.], device='cuda:1'), tensor([3.], device='cuda:1')]
[All-gather] Rank 0 collected: [tensor([0.], device='cuda:0'), tensor([1.], device='cuda:0'), tensor([2.], device='cuda:0'), tensor([3.], device='cuda:0')]
[All-gather] Rank 2 collected: [tensor([0.], device='cuda:2'), tensor([1.], device='cuda:2'), tensor([2.], device='cuda:2'), tensor([3.], device='cuda:2')]
Scatter and Reduce-scatter
Scatter operation is logical inverse of gather operation where data from master rank is distributed or sliced to all other ranks. Gather operation collect data from all other ranks while scatter operation distributes data from one rank to all other ranks.
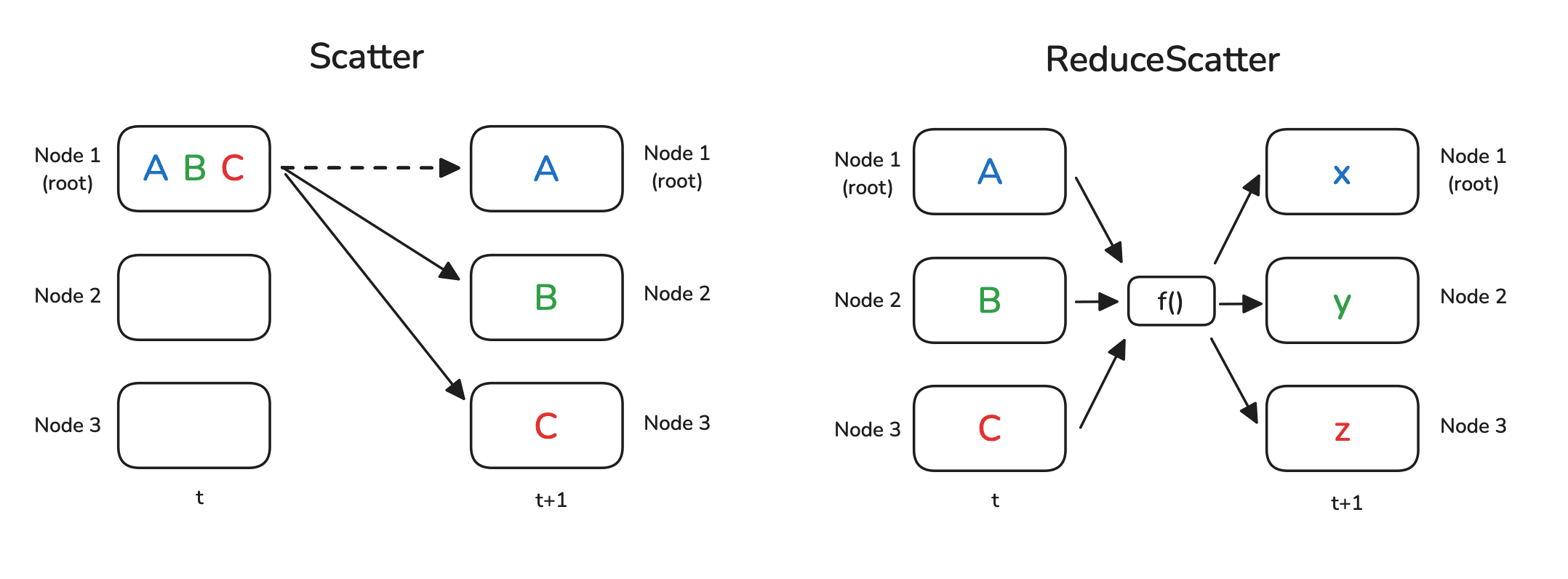
Reduce scatter is widely used algorithm in ZeRO strategies. It is primarily used in ZeRO-2 and ZeRO-3 for averaging gradients and sending each GPU its corresponding partition of averaged gradient. NCCL implements Ring ReduceScatter algorithm to perform element-wise reduction (e.g. sum) across all N ranks. The fully reduced result is then divided into N segments and scattered to each of the N ranks.
import os
import torch
import torch.distributed as dist
def init_process():
dist.init_process_group(backend="nccl")
local_rank = int(os.environ["LOCAL_RANK"])
torch.cuda.set_device(local_rank)
def example_scatter():
rank = dist.get_rank()
world_size = dist.get_world_size()
local_rank = int(os.environ["LOCAL_RANK"])
# Rank 0 prepares data to scatter, others just prepare a placeholder
if rank == 0:
scatter_list = [torch.tensor([i], device=local_rank, dtype=torch.float32) for i in range(world_size)]
print(f"[Scatter] Rank 0 scattering: {scatter_list}")
else:
scatter_list = None
recv_tensor = torch.zeros(1, device=local_rank)
dist.scatter(recv_tensor, scatter_list=scatter_list, src=0)
print(f"[Scatter] Rank {rank} received: {recv_tensor}")
def example_reduce_scatter():
rank = dist.get_rank()
world_size = dist.get_world_size()
local_rank = int(os.environ["LOCAL_RANK"])
# Each rank contributes a tensor of size world_size
input_tensor = torch.tensor([rank] * world_size, device=local_rank, dtype=torch.float32)
print(f"[Reduce-scatter] Rank {rank} input: {input_tensor}")
# Placeholder for reduced chunk
output_tensor = torch.zeros(1, device=local_rank)
dist.reduce_scatter(output_tensor, list(input_tensor.chunk(world_size)), op=dist.ReduceOp.SUM)
print(f"[Reduce-scatter] Rank {rank} output: {output_tensor}")
if __name__ == "__main__":
init_process()
example_scatter()
example_reduce_scatter()
dist.destroy_process_group()
Here’s the expected output:
[Scatter] Rank 0 scattering: [tensor([0.], device='cuda:0'), tensor([1.], device='cuda:0'), tensor([2.], device='cuda:0'), tensor([3.], device='cuda:0')]
[Scatter] Rank 0 received: tensor([0.], device='cuda:0')
[Reduce-scatter] Rank 0 input: tensor([0., 0., 0., 0.], device='cuda:0')
[Scatter] Rank 1 received: tensor([1.], device='cuda:1')
[Scatter] Rank 3 received: tensor([3.], device='cuda:3')
[Reduce-scatter] Rank 1 input: tensor([1., 1., 1., 1.], device='cuda:1')
[Scatter] Rank 2 received: tensor([2.], device='cuda:2')
[Reduce-scatter] Rank 3 input: tensor([3., 3., 3., 3.], device='cuda:3')
[Reduce-scatter] Rank 2 input: tensor([2., 2., 2., 2.], device='cuda:2')
[Reduce-scatter] Rank 1 output: tensor([6.], device='cuda:1')
[Reduce-scatter] Rank 2 output: tensor([6.], device='cuda:2')
[Reduce-scatter] Rank 3 output: tensor([6.], device='cuda:3')
[Reduce-scatter] Rank 0 output: tensor([6.], device='cuda:0')
Reduce and All-reduce
Similar to the gather operation, reduce operation requires all ranks to send data to rank 0. After all data is gathered, it performs summation operation on all the data. Similar to NCCL broadcast implementation, Ring Reduce operation uses chain from ring topology to pass the data. All the data received is reduced and passed to its next neighbor. This process continues until the data reaches the master rank. Finally, the final partial result along with rank 0’s local data is reduced at the master (rank 0 or root).
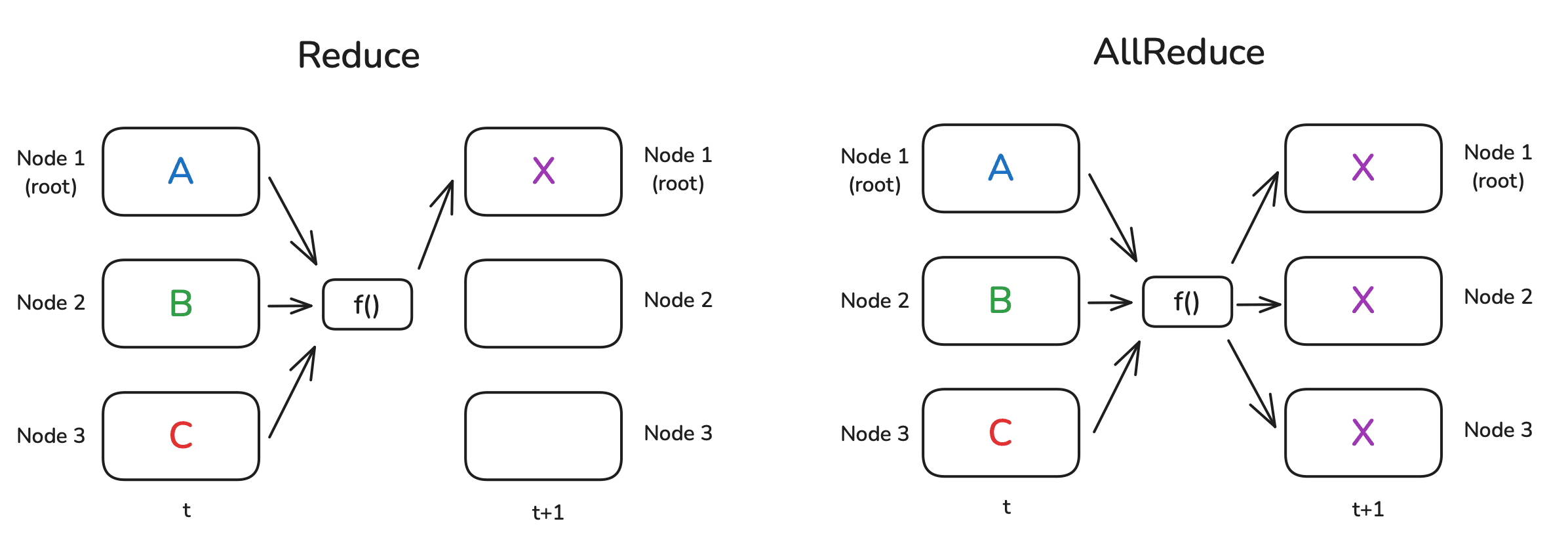
All reduce is the most common collective operation. It is used in both data parallelism and ZeRO-1 sharding strategy. It is used to get final result of gradient before performing optimizer step.
There are two implementations for AllReduce: Tree AllReduce and Ring AllReduce. Ring topology was introduced before where each GPU uses its immediate neighbors (left and right) to form a unidirectional ring. In a tree topology, each GPU keeps track of its parent and child rank. In practice , NCCL dynamically chooses between ring and tree algorithms based on message size and network characteristics: ring for large messages (bandwidth-bound), tree for small messages (latency-sensitive).
Implementation of Ring AllReduce algorithm is a combination of ReduceScatter and AllGather operations. It beings with ReduceScatter operation that perform reduction. The blue portion higlighted in the figure below. It shows how all GPUs have a copy of reduced sum. In next step, AllGather operation makes sure all the reductions are present on all the ranks. The orange portion highlighted in the figure below.
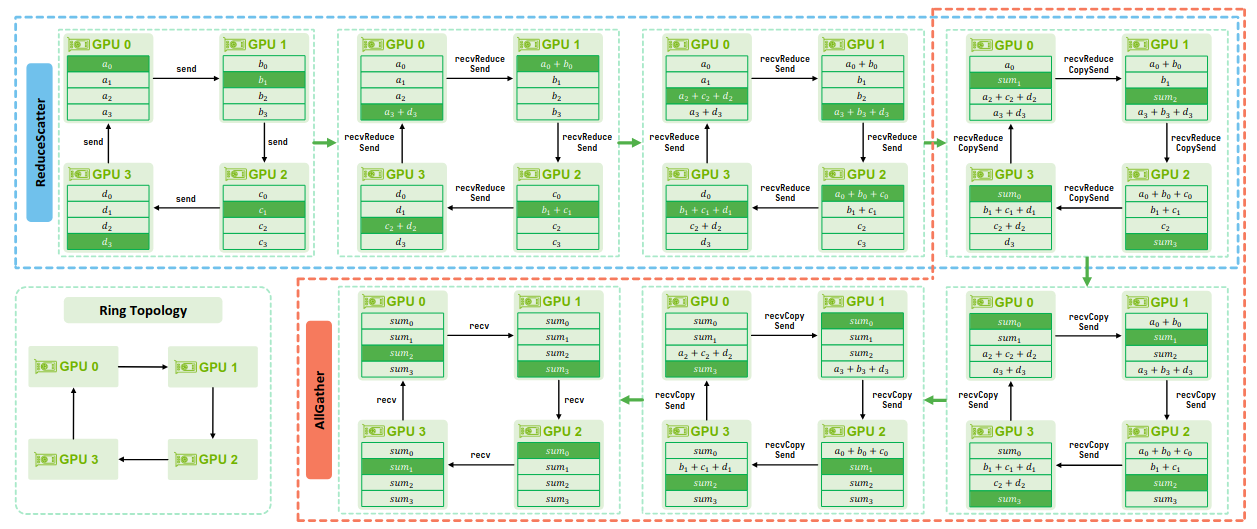
NCCL Paper
Implementation of Tree AllReduce algorithm consists of two phases: Reduce and Broadcast. NCCL build a tree across multiple nodes and within a node it creates a chain for communication. Consider for example in the figure below, there are 4 nodes with 8 GPUs. NCCL would pick 1 GPU per node to form the inter-node tree as shown in the figure. Inside each node, the chosen leader-GPU shares the data with its local GPU via a chain. Here, GPU0 on node0 is the root, GPU2 on node2 is the middle, GPU1 (node1) and GPU3 (node3) are the leaves. In Reduce phase, leaves send the reduce sum upwards towards the root of the tree. And in broadcast phase, the final reduced result is propagated back down the tree from the root.
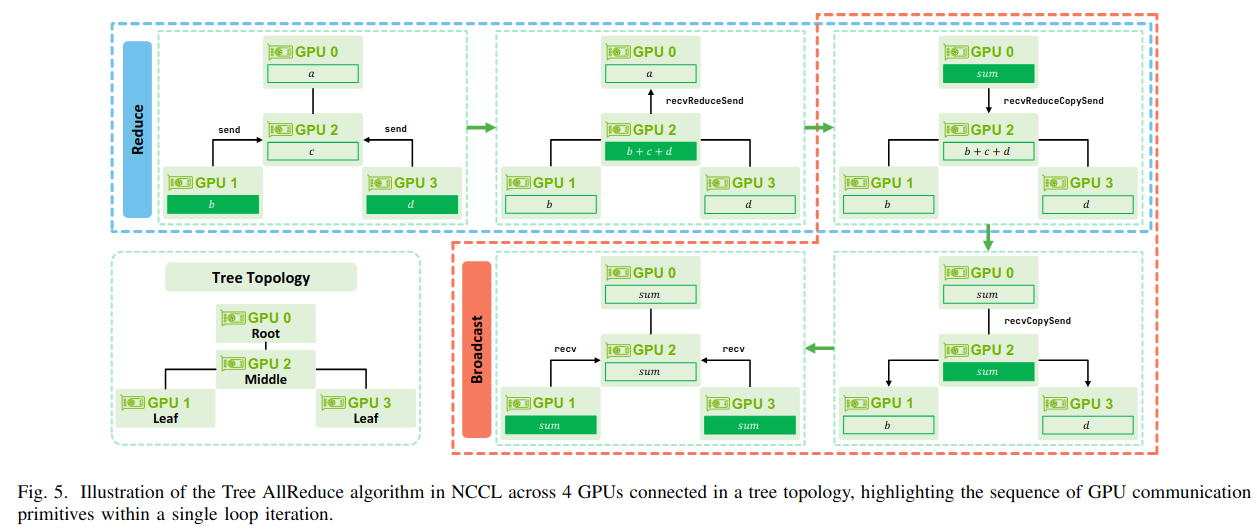
NCCL Paper
import os
import time
import torch
import torch.distributed as dist
def init_process():
dist.init_process_group(backend="nccl")
local_rank = int(os.environ["LOCAL_RANK"])
torch.cuda.set_device(local_rank)
def timed(fn, name=None):
"""Utility to measure runtime of a distributed operation."""
dist.barrier() # synchronize before starting
start = time.time()
fn()
dist.barrier() # synchronize before stopping
end = time.time()
if dist.get_rank() == 0:
print(f"{name or fn.__name__} took {end - start:.6f} seconds")
def example_reduce():
rank = dist.get_rank()
world_size = dist.get_world_size()
local_rank = int(os.environ["LOCAL_RANK"])
# Each rank starts with its ID as a tensor
tensor = torch.tensor([rank], device=local_rank, dtype=torch.float32)
print(f"[Reduce] Rank {rank} starts with: {tensor}")
# Only rank 0 will get the reduced result
output = torch.zeros(1, device=local_rank, dtype=torch.float32) if rank == 0 else None
dist.reduce(tensor, dst=0, op=dist.ReduceOp.SUM)
if rank == 0:
print(f"[Reduce] Rank 0 final result: {tensor}")
def example_all_reduce():
rank = dist.get_rank()
world_size = dist.get_world_size()
local_rank = int(os.environ["LOCAL_RANK"])
tensor = torch.tensor([rank], device=local_rank, dtype=torch.float32)
print(f"[All-reduce] Rank {rank} starts with: {tensor}")
dist.all_reduce(tensor, op=dist.ReduceOp.SUM)
print(f"[All-reduce] Rank {rank} result: {tensor}")
if __name__ == "__main__":
init_process()
timed(example_reduce,"Reduce")
timed(example_all_reduce, "AllReduce")
dist.destroy_process_group()
Measuring runtime around collectives helps reveal the relative cost of different operations. Here’s the expected output for reduce and allreduce operation:
[Reduce] Rank 0 starts with: tensor([0.], device='cuda:0')
[Reduce] Rank 2 starts with: tensor([2.], device='cuda:2')
[Reduce] Rank 3 starts with: tensor([3.], device='cuda:3')
[Reduce] Rank 1 starts with: tensor([1.], device='cuda:1')
[Reduce] Rank 0 final result: tensor([6.], device='cuda:0')
Reduce took 0.195761 seconds
[All-reduce] Rank 0 starts with: tensor([0.], device='cuda:0')
[All-reduce] Rank 1 starts with: tensor([1.], device='cuda:1')
[All-reduce] Rank 2 starts with: tensor([2.], device='cuda:2')
[All-reduce] Rank 3 starts with: tensor([3.], device='cuda:3')
[All-reduce] Rank 1 result: tensor([6.], device='cuda:1')
[All-reduce] Rank 2 result: tensor([6.], device='cuda:2')
[All-reduce] Rank 0 result: tensor([6.], device='cuda:0')
[All-reduce] Rank 3 result: tensor([6.], device='cuda:3')
AllReduce took 0.001405 seconds
As expected, all_reduce is much faster than a plain reduce because it avoids the rank-0 bottleneck
AlltoAll
All to all operation is used by Expert parallelism strategy for training and scaling Mixture of Experts (MoE) models. In this operation, all messages are exchanged by all ranks amongst all ranks. This communication involves a lot of data movement.
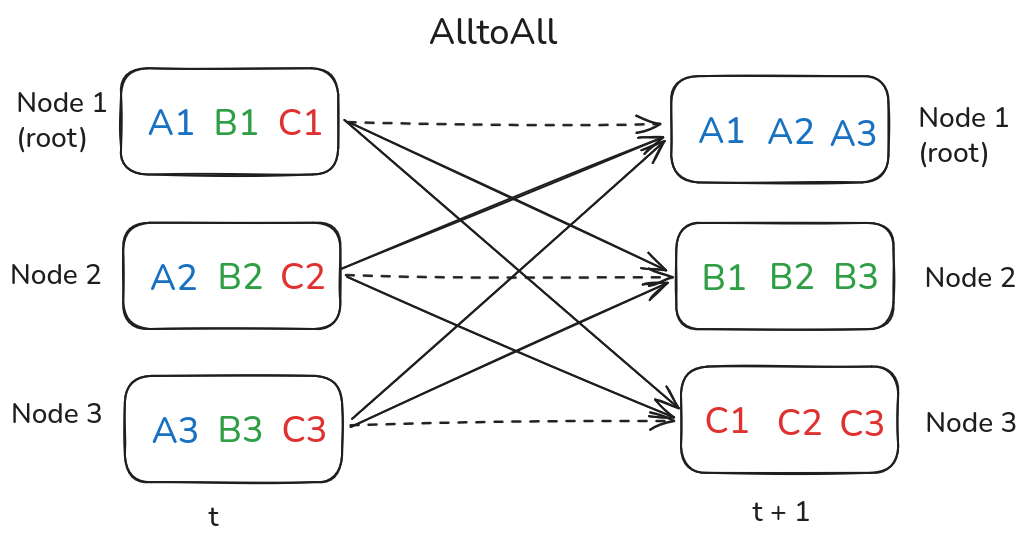
All to all communication
import os
import torch
import torch.distributed as dist
def init_process():
dist.init_process_group(backend="nccl")
local_rank = int(os.environ["LOCAL_RANK"])
torch.cuda.set_device(local_rank)
def example_all_to_all():
rank = dist.get_rank()
world_size = dist.get_world_size()
local_rank = int(os.environ["LOCAL_RANK"])
# Each rank creates a tensor with one value per destination rank
send_tensor = torch.arange(rank * world_size, (rank + 1) * world_size, device=local_rank, dtype=torch.float32)
recv_tensor = torch.zeros(world_size, device=local_rank, dtype=torch.float32)
print(f"[All-to-all] Rank {rank} starts with: {send_tensor}")
# Split into chunks and exchange
dist.all_to_all_single(recv_tensor, send_tensor)
print(f"[All-to-all] Rank {rank} received: {recv_tensor}")
if __name__ == "__main__":
init_process()
example_all_to_all()
dist.destroy_process_group()
Here’s the expected output for AlltoAll:
[All-to-all] Rank 3 starts with: tensor([12., 13., 14., 15.], device='cuda:3')
[All-to-all] Rank 1 starts with: tensor([4., 5., 6., 7.], device='cuda:1')
[All-to-all] Rank 2 starts with: tensor([ 8., 9., 10., 11.], device='cuda:2')
[All-to-all] Rank 0 starts with: tensor([0., 1., 2., 3.], device='cuda:0')
[All-to-all] Rank 0 received: tensor([ 0., 4., 8., 12.], device='cuda:0')
[All-to-all] Rank 1 received: tensor([ 1., 5., 9., 13.], device='cuda:1')
[All-to-all] Rank 3 received: tensor([ 3., 7., 11., 15.], device='cuda:3')
[All-to-all] Rank 2 received: tensor([ 2., 6., 10., 14.], device='cuda:2')
Practical Use Cases
Different collective operations are widely used in distributed training workflows:
- Broadcast → Parameter initialization
- All-gather → ZeRO optimizer state sharding
- All-reduce → Data parallelism
- Reduce-scatter → Gradient averaging in ZeRO-2/3
- All-to-all → Routing tokens in Mixture of Experts
Wrap up
Distributed training relies heavily on efficient communication between GPUs. Point-to-point operations, such as send and recv, provide flexibility for pipeline parallelism, while collective operations like broadcast, all_reduce, and all_to_all are the backbone of data parallelism, ZeRO strategies, and Mixture-of-Experts models. For example, broadcast is ideal for sending initial model weights once, all_reduce efficiently aggregates gradients across GPUs, while all_to_all supports token routing in MoE layers.